Bayesian Evidence Calculation

In a Bayesian framework, object classification or model comparison can be done naturally by comparing the Bayesian evidence between two or more models, given the data. The evidence is the integral of the likelihood of the data over the entire prior volume for all the model parameters, weighted by the prior. (The ratio of evidence for two different models is known as the Bayes Factor.) This multi-dimensional integral gets increasingly computationally intensive as the number of parameters increases. As a result, several clever algorithms have been developed to efficiently approximate the answer.

In this hack, I looked at a couple specific implementations of such algorithms in Python.

Thermodynamic integration in Emcee

Parallel tempering is one way to calculate evidence. Dan F-M's excellent Python package Emcee includes a PTSampler (PT = parallel tempering) that has a method PTSampler.thermodynamic_integration_log_evidence() for performing the evidence integral after the sampler is run. Phil Marshall ran the sampler on the test problem from the docs, wherein the likelihood function is simply a mixture of two 2-d gaussians and the prior is uniform. For this simple function, the evidence can be calculated analytically, so the result from PTSampler can be checked.

As detailed in an Emcee pull request it turned out that the PTSampler result didn't match the analytic solution. This appears to be a bug in PTSampler! It's now handed off to one of the Emcee developers.

Nested sampling in Nestle

Nested sampling is another algorithm for calculating evidence. There are a number of variants on the method. Without going into it in detail, the nested sampling algorithm employs a population of "active" points sampling the parameter space. The variants are chiefly concerned with efficiently choosing a new active point from the region of parameter space occupied by the current active point, without being biased by the existing points.

MultiNest is a popular implementation of one variant, and there is even a Python wrapper for it. While MultiNest is free for academic use, it doesn't have a truly open-source license, making widespread distribution and installation more complicated.

Single-ellipsoidal variant

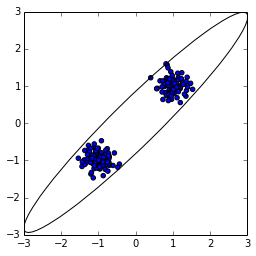
I was motivated by the MultiNest licensing issue to make available my own simple pure-Python implementation of nested sampling in a package called Nestle (rhymes with "wrestle"), tuning up the docs and implementing an automated test. Nestle currently implements a "single-ellipsoidal" variant of nested sampling, where a single ellipsoid is drawn around active points, and a new active point is picked uniformly from within the ellipse. This works well when the likelihood is unimodal: the single ellipse is a good approximation to the region occupied by the points. Unfortunately, the method suffers when the likelihood is multimodal. When this happens, the active points form multiple clusters in parameter space. Shown at left is what happens when you draw a single ellipsoid around such points. When you then chose a new point uniformly from within this ellipse, you're most likely to pick a point nowhere near the active points (and probably with lower likelihood than all the active points). You then have to keep picking new points from within the ellipse until you happen to get a good one.

Multi-ellipsoidal

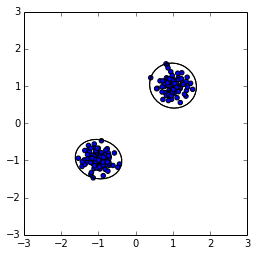
The solution implemented in MultiNest is to try to detect clusters of points and draw multiple ellipsoids around the clusters (see right figure). Picking a point from within these two ellipses is much more likely to yield a point near the existing active points. However, finding clusters robustly is non-trivial.

Future

I plan to keep working on Nestle, for use in my own projects and to make it available to others. Here's a rough to-do list:

• Make the original "MCMC" sampling variant available as an option.
• Make the multi-ellipsoidal sampling available as an option, possibly using the X-means clustering algorithm.
• Speed ups if necessary, using Cython.
• I'd like to have a Julia implementation as well.